从电子表格到R语言

之前，我写过一篇关于体育博彩行业性质发生变化，会员们必须提高自己的技能以跟上变化的文章（《欧洲庄家的体彩变革》）。我自己所采取的一种方法是学习用R语言来进行数据分析。我们每天都使用统计知识，我知道许多体博网会员已经精通R语言。然而我相信，还有很多人像我一样，分析工作一直局限于微软的电子表格。我们觉得使用电子表格最舒服，改用类似R语言的平台的这种展望似乎令人生畏。

相对于电子表格，R语言在分析和建模上有许多优点，我希望在这里证明一下这些优点，它们包括速度、规模、图形化能力、运算脚本。这意味着将来可以很容易地（由自己或其他人）复制运算。许多行业的雇主都越来越喜欢拥有R语言技术的雇员，拥有传统的电子表格技能的候选人越来越不受重视了。

如果你使用电子表格中复杂的公式很上手，那么过渡到R语言可能不会像你想的那样痛苦。如果你在应用R语言的过程中遇到困难，你可以访问一个巨大的支持网络，下载一系列的免费软件包，这意味着许多令人畏惧的、大量的代码通常已经为你写好了，包括具体的运动模型软件包，这些软件包是基于Dixon和 Coles (1997)、Karlis和 Ntzoufras的知名足球评级模型而开发的。

有很多免费的在线课程，我选择的是着重展示R语言应用的统计课程（避免任何太注重编程的课程）。我选择的课程很好地介绍了R语言在体育中的应用，Coursera上也有一门优秀的通用《统计学》课程。

我目前正在学习《统计学习》课程，我希望能够在未来的文章中涵盖这些更先进的技术。现在我想对比电子表格、演示一下R语言的功能，我将分析在英格兰足球比赛中旅行距离和主场优势之间的关系。

为什么要分析旅行距离和主场优势之间的关系？

主场优势仍然是一个有趣但却遭到误解的概念。关于主场优势的存在已经提出了许多解释，其中之一是客场球队旅行距离对主场优势的影响。由于节日期间大量固定比赛的投注需求，这个问题最近受到了广泛关注。

数据集

该数据集包含了从www.football-data.co.uk网站上获得的英格兰足球5个完整季节的结果（包括英超联赛和乙级联赛的10180场比赛）。为凸显主场优势，我们将主队、客队配对显示结果，这样每一个赛季有5090行数据。数据的样本如下：

例如：2008 / 09赛季，阿森纳队在主场4:0击败布莱克本队，客场也以4:0获胜。主场优势（AvgMargin）总是从主队角度考虑，因此这对球队的结果是((+4-4)/2) =0。在对阵埃弗顿队的比赛中，阿森纳在主场取得3:1的比分，客场1:1战平。这对组合的主场优势是+ 1。

在这种统计方式中，结果是成对的，以消除球队之间的不同能力水平的影响。例如，把卡莱尔队和阿森纳队的比赛同卡莱尔队和巴尼特队的比赛同等对待是不公平的。同样，结果只在单赛季内配对比较，以消除球队能力水平波动的影响；卡莱尔队在2008 / 09赛季和2012/13赛季到朴茨茅斯的旅行是两次非常不同的旅行。

根据Wayne Winston教授的理论，计算每对球队组合的路程。距离都以英里为单位进行记录，且都是计算直线距离（如同计算乌鸦的飞行距离）。

该数据（csv格式）和R语言分析脚本（txt格式）可以从下面的链接下载：

Data

R Script

检查数据

下一步是更仔细地检查数据（如检查分布和均值、检查异常值等）。

一行代码生成了一个主场优势变量的柱状图（图1）：

> hist(AvgMargin, col = “red”, breaks = 20)

（*注意：这行代码的语句与电子表格公式非常相似）

图1

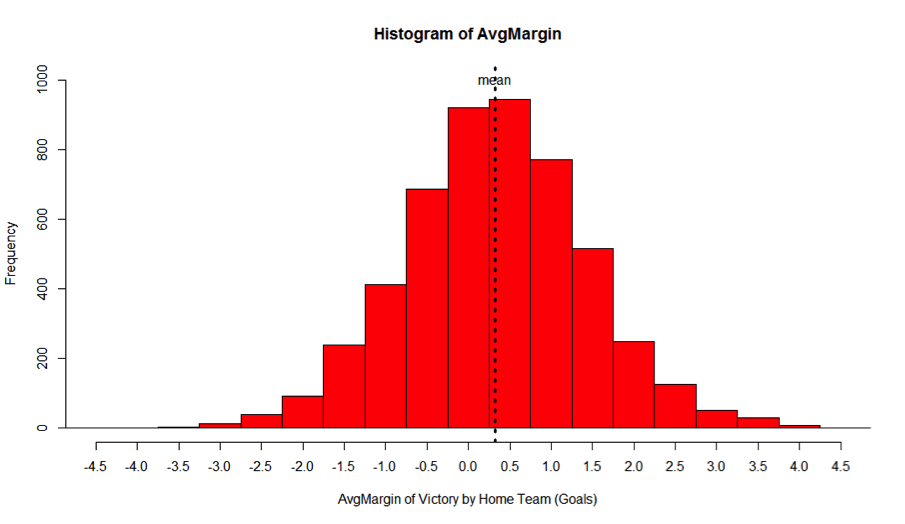
（* 电子表格中相同的函数计算更费时，[http://www.youtube.com/watch?v=RyxPp22x9PU]）

最常见的主队主场优势值是零和 +0.50球。主队主场优势的平均值是+0.33球。

距离变量的汇总统计也可以用一行代码来查看：

（*用电子表格来进行上面的计算需要几个不同的公式）

距离从0到335英里不等，均值为116英里，中值为112英里。

是否有证据表明距离和主场优势之间存在某种关系？

首先，距离变量被分为两组：低于中值组（112英里）和高于中值组（见图1）。应用塔普利函数重新计算每组主场优势的均值：

（*在电子表格中，这必须借助数据透视表或Sumif和Countif公式）

所有旅行距离不足112英里的配对组合中，主队主场优势是+0.28球。所有旅行距离超过112英里的配对组合中，主队主场优势是+0.37球。这差别可能不是很大，但在博彩中，这可是到底投注还是不投注的决定因素。

为了使这个差异更直观，也顺便展示R语言的图形功能，我们生成了一个频率多边形（图2）：

>ggplot(Matches, aes(AvgMargin, colour=Median)) + geom_freqpoly()

图2

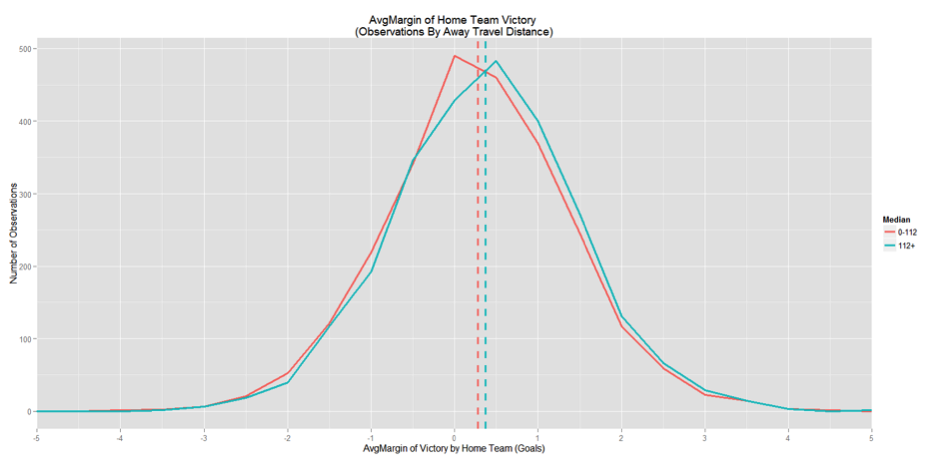
图2中两条实线代表观察到的每个可能的主场优势，分成旅行距离超过中值112英里（蓝线）和不足中值112英里（红线）两组。垂直虚线代表两组各自的均值（+0.28和+0.37）。我们看到超过112英里的这组中，均值稍高、观察到的主队主场优势较多（即零右侧蓝线上每一个值都高于红线）。零左侧每个主场优势值是相反的情况。

可以观察到旅行距离和主场优势之间存在一个微弱的关系。然而，这也可能是由于偶然或抽样误差。我们可以通过t检验来验证统计显著性：

（* 在电子表格中验证显著性需花费更多时间  [http://www.youtube.com/watch?v=norKDF0MH0M]）

这里要注意的是P值= 0.00438。这个数字表示，如果旅行距离和主场优势之间没有关系，从这个特定的数据集中观察到这种差异的机率（0.28和0.37之间）（即在这个数据集中如果旅行距离和主场优势之间没有实际的关系，只会有0.4%的机率会发现我们所观察到的差异）。

一旦观察到某种影响，有必要去估测这个影响的大小。在R语言中利用科恩D函数去进行估测：

（* 在电子表格中，此计算过程要慢很多 [http://www.youtube.com/watch?v=OBQIKIcrAGI]）

科恩D的得分如果是0.079，则证明影响非常小。观测到的关系是显著的（这不可能是随机观察到的），但这似乎没有对结果变量——主场优势形成非常大的影响（即它只是起作用的可解释变量之一）。

绘制线性模型

以中值分割数据也是有问题的。因此，还需创建一个简单的线性回归模型来囊括全距离变量。

下面的语句进一步证明了R语言的图形功能：

>ggplot(Matches, aes(x=Distance, y=AvgMargin)) + geom_smooth(method=”lm”)

图3

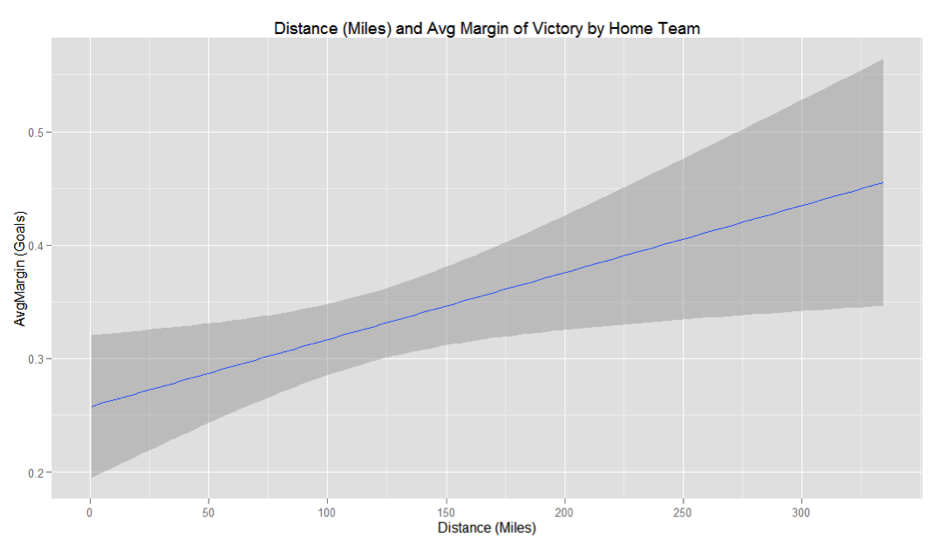
（*在电子表格中，此过程要慢很多 [http://www.youtube.com/watch?v=aSOUQKqIYak]）

图中向上倾斜的蓝色回归线区域显示，随着距离的增加（X轴），主队的主场优势也增加（Y轴）。深灰色阴影区域代表围绕这条回归线的95%置信区间。

线性模型的全部细节如下

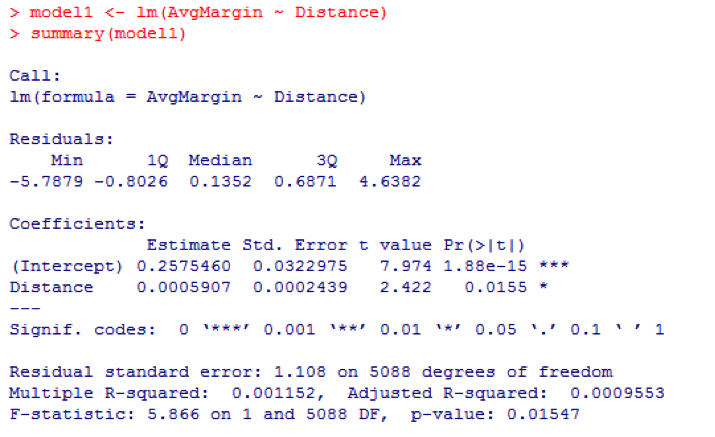
截距（intercept + 0.257）表示当模型认定旅行距离是零时一对球队组合的主场优势（见图3）。在截距（intercept）下面的数字+ 0.00059，是回归系数。它表示，旅行距离每增加1英里，主队的主场优势将增加0.00059球。这个数值的P值是0.015，表示这种关系是显著的（即我们观察到的不太可能是随机现象）。

另一个需要注意的数值——多平方值是0.001152。它表示主场优势方差与旅行距离方差的比。这意味着，只有约1%的主场优势可以用距离旅行来解释。下面全尺寸的散点图可以让此概念更一目了然：

图4

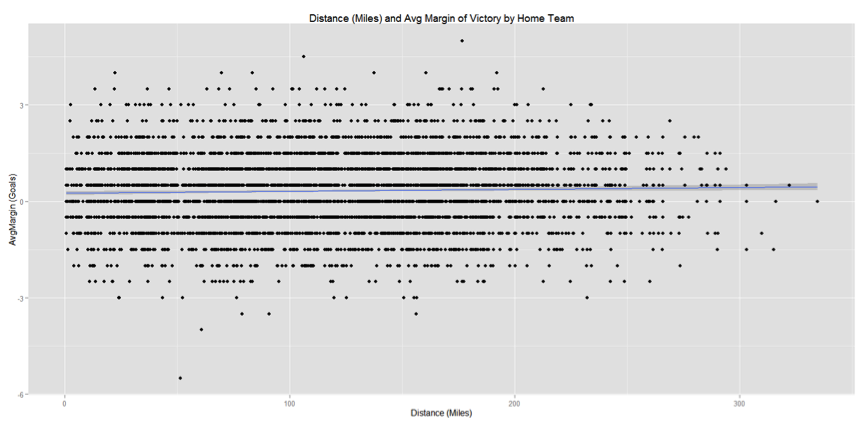
这张图呈现的是旅行距离和主场优势之间的多平方值的完全分布。线性模型的回归线是很浅的，观察到的结果周围呈现出一个很宽的方差区域。因此，想要用该模型充分预测一场足球比赛，还需付出更多的努力。

结论和下一步的工作计划

以上分析表明，旅行距离和主场优势之间存在某种关系，虽然这种关系的影响作用非常小。这种关系只是影响一场足球比赛结果的不同变量之一。而在博彩中，正是这细微的不同左右了下不下注的决定。所以，在设计更复杂的预测模型时，把旅行距离和其它变量一起纳入模型中还是有必要的。

关于进一步的分析，我有几个想法。作为变量，胜利优势可能会有一定的局限性，所以可以尝试使用比赛结果（赢——平局——负）作为变量。而且，有可能其它因素也会影响旅行距离的作用。例如，旅行距离的影响是不是由于不同的分组有不同的效果呢？会不会有季节性的影响？旅行距离对周末比赛与非周末比赛会有不同的影响吗？

最后的评价

谢谢你读我的文章，希望我所说的向你证明了，R语言并不像乍看上去那样令人生畏。我也希望我已经证明了，弃电子表格而用R语言会带给我们一些直接的好处。对于那些已经使用了R语言的会员，请随便下载数据以方便你自己的工作。我也衷心希望你能对上面的内容提出改进的建议，毕竟促进合作才是建立体博网的宗旨。