What is the favourite-longshot bias?

The favourite-longshot bias is a widely examined phenomenon in sports betting analysis, and is shown to have existed across many sports and leagues. The favourite-longshot bias explains that the odds offered on favourites provide better bets for bettors than those on longshots, despite potentially both having negative returns.

The bias is usually explained as being caused by bettor irrationality. Bettors are said to prefer a low probability, high payoff bet (longshots). These are therefore over bet, and bookmakers react by shortening their odds.

What role does the bookmaker play?

In this article, I examine whether the favourite-longshot bias could arise from bookmaker rationality, by considering odds setting from the bookmaker’s perspective. How might bookmakers apportion the margin between the favourite and the longshot? Is there an optimal strategy?

Let’s assume a bookmaker is a perfect forecaster. In a two-way contest they accurately determine the probabilities to be 20% and 80%. Thus, the fair odds are 1/0.2 = 5.0 and 1/0.8 = 1.25. If the bookmaker wants a 3% margin, the odds they offer will fall somewhere between 5.0, 1.205 (all the margin in the favourite) and 4.35, 1.25 (all the margin in the longshot). Somewhere along the line below.

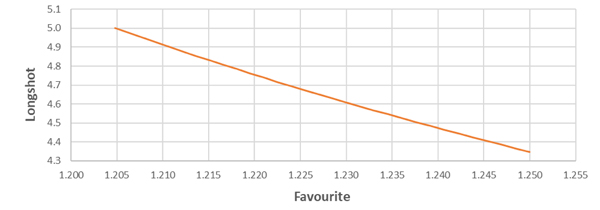
The chart below plots the expected return to a bettor when placing a bet on either the favourite or longshot within this range.

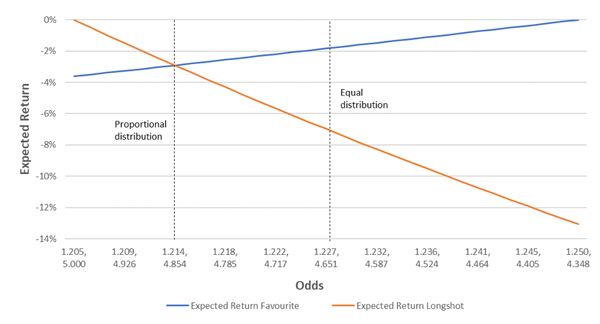
If the bookmaker apportions the 3% margin equally (1.5% each side), the prices offered will be 1.227 and 4.651. The expected return from a bet on the favourite is -1.8%, and on the longshot is -7.0%. With this choice of margin distribution, a favourite-longshot bias in the odds is created.

The point at which the expected returns are equal (where the lines intersect) is where the margin has been distributed proportionally, relative to the true probabilities. 80% in the favourite (2.4%) and 20% in the longshot (0.6%). If the bookmaker chooses any odds combination to the right of this point (a shorter longshot), a favourite-longshot bias will be expected.

That is, a bet on the longshot will have a lower expected return than a bet on the favourite. The chart below plots the expected return for a bettor when betting into odds with a 3% margin, for a proportional and equal margin distribution.

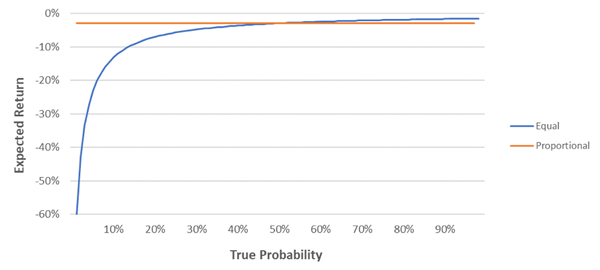
If the margin is distributed proportionally, the expected return from a bet at any odds will be the same, and we would expect no favourite-longshot bias. If the margin is distributed equally however, we would expect a strong one. That is, lower expected returns at lower implied probabilities. Therefore, without knowing how a bookmaker apportions the margin, any proposed reason for a favourite-longshot bias in odds is tenuous at best.

The bookmaker’s perspective

Returning to the example of a contest with true probabilities of 20% and 80%, let’s assume bettors bet an aggregate 50% of money on both the favourite and 50% on the longshot. In the chart below the grey (green) line plots total bettor (bookmaker) expected return. With an even split of money wagered, the bookmaker would maximise their expected return by pricing the favourite as long as possible, and therefore the longshot as short as possible.

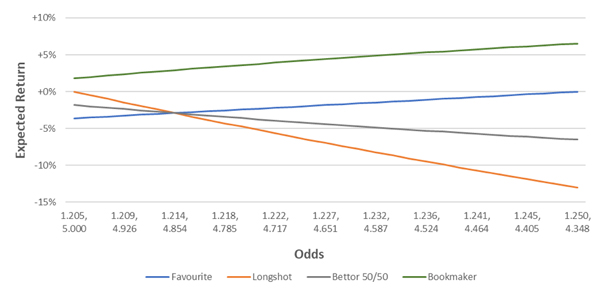
What if the money wagered on each side isn’t even? The chart below shows the bookmaker’s expected return for different proportions wagered on the favourite. The orange line for example, plots the bookmaker’s expected return from a 70:30 split between favourite and longshot.

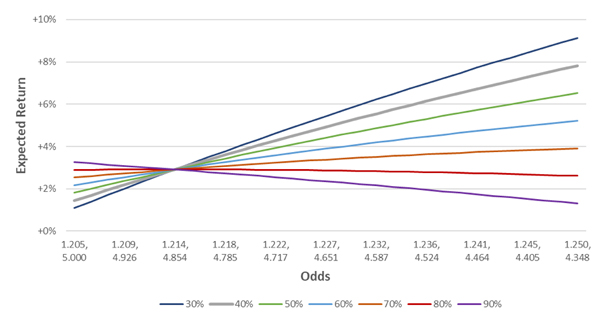
Without knowledge of the proportion wagered on each side, it would appear that a simple strategy of drifting the favourite and shortening the longshot is a good one for a bookmaker. So long as the bookmaker can attract a higher proportion of bets on the longshot than the true probability (in this case 20%), they have an incentive to shorten the odds of the longshot, to increase their expected return.

What happens when we adjust the risk?

Adjusting returns for the risk taken on to produce them is a financial concept known as “risk adjusted return”. Taking on more risk requires compensation via a higher expected return. Similarly, for two scenarios with equal expected returns, the better proposition is the one that is less risky.

With imperfect forecasts, the financial penalty to a bookmaker for being inaccurate will likely be greater for longshots at higher odds.

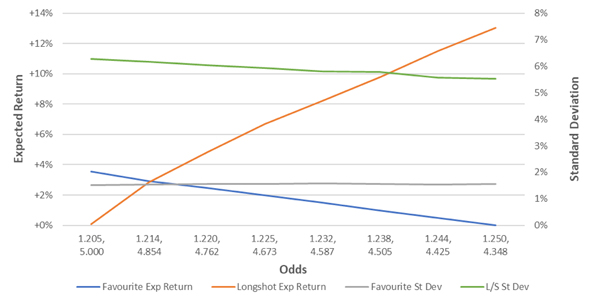
Let’s assume a bookmaker distributes the margin proportionally in the above example, thus setting odds of 1.21 and 4.85. We know that the expected return for a bookmaker is the same at these odds, +2.91%. What would a bookmaker prefer? 1,000 bets on the favourite or 1,000 bets on the longshot? Let’s analyse variance.

To do this, I simulated a series of 1,000 bets on the favourite and longshot, 5,000 times each, and calculated the standard deviation of returns. For bets on the favourite the standard deviation of returns was 1.5%, and on the longshot was 6.2%. A rational bookmaker would no doubt prefer to lay the favourite, as the risk is lower.

If a bookmaker would prefer to lay the favourite when the expected returns are the same, it follows that they would want to drift the favourite’s price, and shorten the longshot. Where they become indifferent is where they may want to set their odds. Solving this problem will depend on a particular bookmaker’s risk appetite, however we can plot the expected returns and standard deviations at different margin distributions to understand their potential decision.

Consider the odds 1.220, 4.762. What would a bookmaker prefer? Laying the favourite (2.5% expected return and 1.6% standard deviation) or the longshot (4.8% expected return and 6% standard deviation)? Let’s plot the returns from the 5,000 simulations at these prices.

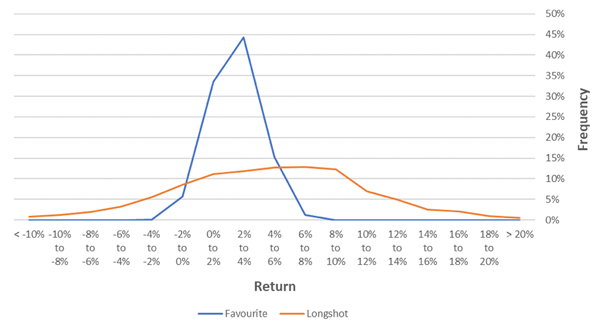
The decision is less straightforward. In any case, drifting the favourite and shortening the longshot from the proportionally distributed margin (1.21, 4.85) will introduce a favourite-longshot bias into the odds.

Now let’s vary the proportion of money wagered on each side. Following the same example, assume again that a bookmaker accurately determines probabilities of 20% and 80% in 1,000 independent events, and is deciding where to set the odds (maintaining a 3% margin). One 1-unit bet is placed on each event, and the bookmaker’s total return is calculated. I simulated this scenario 5,000 times for varying proportions of bets on the favourite and longshot. The average return and standard deviation of returns is plotted in the chart below.

The number above each point is the proportion of bets on the favourite. For example, consider the yellow line at point 0.5. This point represents the average return (4.5%) and standard deviation (4.3%) with prices 1.23 and 4.65, when 50% of bets were on the favourite.

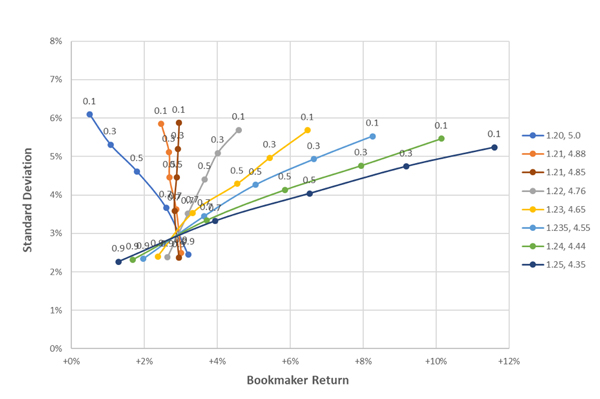
Let’s assume this point represents a bookmaker’s current odds pricing strategy and proportions wagered. If they changed the odds and the same proportion is wagered on each side, shortening the favourite (say to the grey line, 1.22 4.76), would reduce their expected return (to 3.7%) and increase their standard deviation (to 4.4%). It’s unlikely they would choose to do this.

Alternatively, shortening the longshot (say to the light blue line, 1.235 4.55) increases the expected return (to 5.0%) and reduces the standard deviation (to 4.25%).

Adjusting returns for the risk taken on to produce them is a financial concept known as risk adjusted return. Taking on more risk requires compensation via a higher expected return.

As such, if the proportion wagered on each side remains constant, the bookmaker has an incentive to shorten the longshot from both an expected return and risk perspective. Again, this holds true so long as the proportion of money wagered on the longshot exceeds the true probability (in this case 20%).

What if bettors demonstrate some price (odds) sensitivity? That is, if odds increase, a higher proportion of money will be wagered on that outcome. From the same starting point, If the bookmaker decides to drift the favourite’s price from 1.23 to 1.24 (yellow to green line, longshot 4.65 to 4.44) we would expect a higher proportion of money wagered on the favourite.

This proportion can increase from 50% to 62% before the bookmaker would expect a reduction in expected return, whilst simultaneously benefiting from a reduction in standard deviation (from 4.3% to 3.7%).

What have we learnt about favourite-longshot bias?

The analysis in this article suggests that introducing a favourite-longshot bias in the odds they offer will often be a rational strategy for a bookmaker, from a risk adjusted return perspective. While the examples were predicated on a bookmaker being a perfect forecaster, relaxing this assumption should only strengthen this conclusion.

With imperfect forecasts, the financial penalty to a bookmaker for being inaccurate will likely be greater for longshots at higher odds. This may be especially true for bookmakers such as Pinnacle with a high proportion of sharps, and high limits.

While it may be rational for a bookmaker to introduce a favourite-longshot bias in their odds, they will also have the added benefit of understanding the betting preferences of their clients.

This information will assist further in optimising their risk adjusted expected return when setting odds and distributing the margin. In any case, odds containing a favourite-longshot bias may not solely be the result of bettor biases. They are just as likely to be a result of bookmakers being rational, informed, financial risk managers. However, I presume it’s a usually a combination of both.