Related Articles
Related Jobs
对于固定赔率下注,“赔率”这个概念往往指的是价格,是赌博玩家们能够赢到手的钱。但是对于赔率来说,还有一个更传统的意义,那就是它能够帮助我们更好的理解概率和下注。
在统计学里,有利的赔率,也就是我们所熟知的赔率,它代表了事件发生概率与不发生概率之比。假设p为事件发生的概率,那么这个事件的比值则可以表示为:
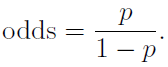
举个例子,假设事件A的发生率为0.4,那么事件A的赔率就为2/3。同样,事件的反比值即事件不发生的概率与发生概率之比。如果事件A的赔率记为odds(A),事件B的赔率记为odds(B),则可以定义A对于B的赔率比为
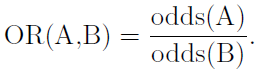
赔率比这个概念一般用来计算两个事件间的相互概率,如果事件A对事件B的比值比为2,那么就可以断定事件A发生的概率两倍于事件B。为了更好的说明这一点,这里对50%与51%之间,98%与99%之间的差别进行比较。从绝对值的定义上看,上述两组数据之差都为1%,但是从直观上来看,98%与99%的之间差别比50%与51%的差别要大得多。51%对50%的赔率比为1.04,但是99%对98%的赔率比为2.02,因此可以看出后者之间的差别确实比前者要大一些。同样从直观上来看,60%是30%的两倍概率,但是我们无法从直观上看出60%的两倍情况。通过运用赔率比,可以得出75%是60%两倍概率的结论,因为75%对60%的赔率比为2。
在现实生活中,赔率与赔率比的运用体现在博彩公司对优势比的分配上,优势比代表了博彩公司的利润率。假设在博彩市场上的某一个事件里,唯一的赢家将从n种选择中产生,对于庄家开出不同的价格o1, o2一直到on来说,优势比的定义为所有价格的赔率倒数之和:
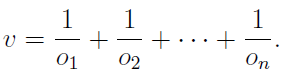
假设所有赌注在所有可下注选择上按恰当的比率分布,那么优势比则代表了庄家需要通过单一币种来支付的返奖额。进一步来说,对v=1.081时,如果庄家以合适的比率设置10.81镑,那么他们需要付给赌众10镑。对于优势比来说另一个重要的概念是,下注市场的利润毛利m,它被定义为假设赌注按正确比例分布的条件下,庄家在总收入里纯利润的百分比。毛利与优势比关系如下:

博彩公司是如何定价(对于真实价值来说)来获取利润的,这个问题的答案并不唯一,但是随着自动下注模型的诞生,找到一定的算法来合理分配优势比,这一需求确实一致的。
假设一个简单的有正反两种情况的市场存在,正面性的概率为p,负面性的概率为1-p,这就意味着p+q=1。当按算法来分配优势比时,我们需要用函数f和g来表示概率p与q,相对的,f(p)+g(q)=v,这里v即overround。对函数的选择中有一种情况为f(p)=vp并且g(q)=vq(这种情况下f(q)+g(q)=vp+vq=v,满足条件)。这种方法实际上称之为比例分布,它表示了按所期望的优势比对真实赔率进行简单拆分。由于其简单易于运用,这个方法在业内耳熟能详,但是当正面性事件概率较高的时候,这个方法产生的最终概率会出现大于1的情况。另一种方法是将优势比均为分配到两种相对的概率上,即f(p)=p+0.5(v-1)与g(q)=q+0.5(v-1)。同样,优势比的条件也是成立的。这种方法看上去优于比例分配的办法,但是仍然会出现概率大于1的问题。第三种方法可以保证最终概率在0到1之间,这种方法使用了赔率与赔率比的概念。
假设优势比函数f与g将真实概率p与q代入新概率x与y中,要对优势比进行分配,一个合理的途径是需要保证概率p与x,q与y之间的差异“相等”。我们现在介绍的方法将保证这些成对的新旧概率之间的赔率比相等,即
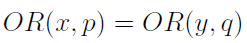
假设赔率比为c,那么
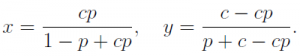
如果定义x+y=v,那么就可以对c进行求解,并由此得到x与y的最终表达式。如下的表格中给出了通过上述分布方法计算得出的毛利为0.075的两面市场中真实赔率与新赔率。
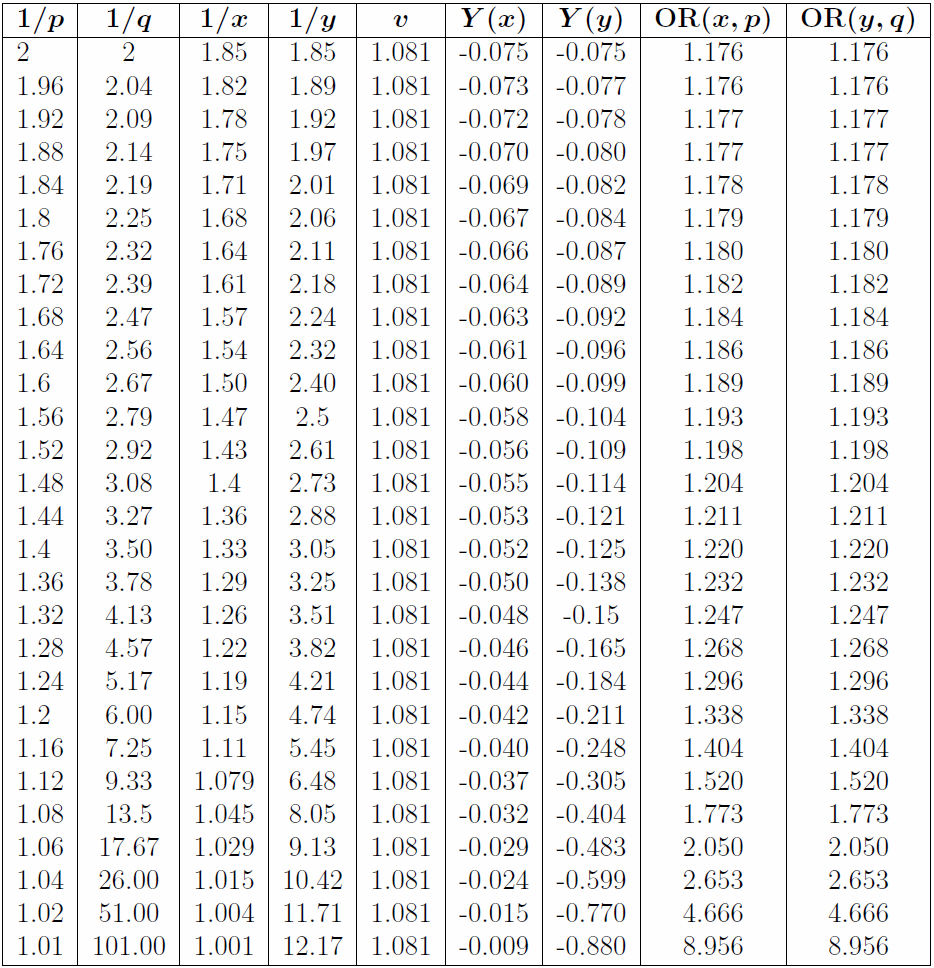
需要注意的是,对于每一对赔率来说优势比是一样的。用Y来表示(赌博玩家的)产量,即回报率,它是按赌注百分比来表示的赌博玩家下注的期望盈利或亏损。如果o是庄家的赔率,ot是真实赔率,那么它们之间的关系可以表示为
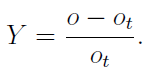
如果某个事件的真实赔率为1.6,它的开价为1.5,一位玩家对其下注1镑,那么其回报率就为-0.06或-6%,这就意味着他可以赢回0.94镑。值得注意的是,按这种方法对优势比进行分配,短期下注所产生的回报率比长期下注要高。同样,x对p与y对q的赔率比相等,这些赔率比随着概率的增加也变得不再一样。这就意味着,举例来说,(1.08, 13.5)与(1.045, 8.05)之间的差别比(1.8, 2.25)与(1.68, 2.06)之间的差别要“大”,尽管这两对数据的优势比是一样的。这就可以看出,在拥有相同优势比的情况下,赔率不均的市场所拥有的“价值”比赔率更均衡的市场要低。为了弥补这个问题,庄家们逐步压低优势比以减小概率之间的差异。对于优势比的分布,我们同样可以运用这种方法来消除优势比。这里可以为比例分布编制同样的数据表格来进行比较,毛利仍为0.075。
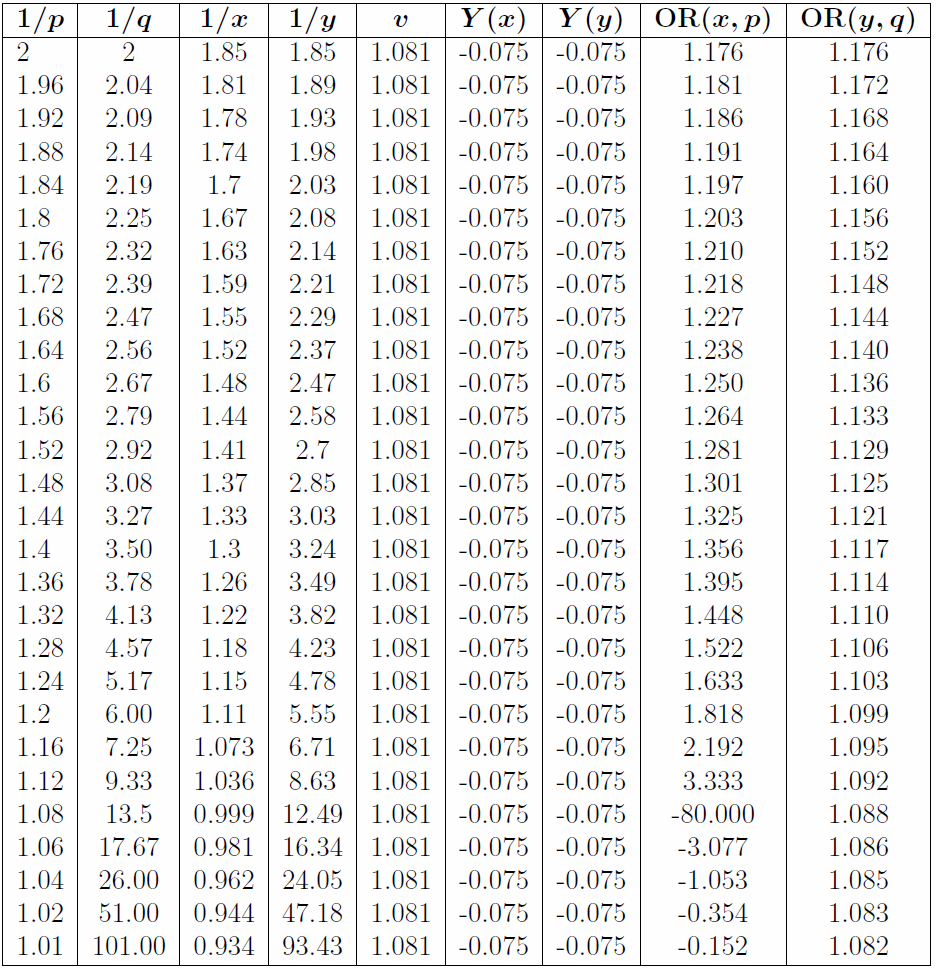
同样,每一对比值的优势比是一样的,对每一种选择来说庄家的回报率即为毛利,这是比例分布的重要特性。通过比例分布可以看出过多的优势比被分配到了强势上,而分配到弱势上的优势比不足,最终导致概率值超过1。通过对比值比的分析可以帮助我们理解其中的问题所在,我们可以看到当比值少的时候比值比增加,当比值小于1的时候比值比变为负数;比值多的时候比值比减少,这就意味着新的比值逐渐接近真实的比值。
如果一家博彩公司希望赔率能够到使每单位赌注都会产生相同的回报率,唯一的途径是通过比例分布,但是很明显这并不是一个设定赔率的好办法。我们已经看到,相同的比值比是设定最终赔率的更好的办法,但是(至少在两面选择的情况下)它的特点是赌徒在低赔率上下注所产生的回报率比在高赔率上下注要多,同样该回报率随着赔率的减少急剧增加。显而易见,无论事件中有多少种可供选择的条件,相同的比值比会都使产生这个现象。对低赔率下注所产生的回报率高于高赔率这个特性有时被称为 favourite–longshot 偏差。由于庄家们的赔率制定规则, favourite–longshot 偏差主要存在于固定赔率下注市场中,庄家所参照来制定赔率的方法(考虑所有会对赔率造成影响的因素)将很可能造成最终赔率称为 longshot 偏差。
