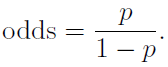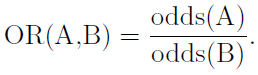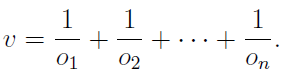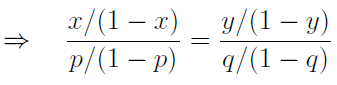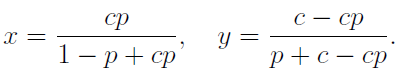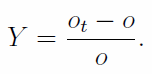Related Articles
In fixed-odds betting, the concept of ‘odds’ generally refers to the price, the amount the punter gets back if the bet wins. However, there is another, more traditional, definition of odds – one that can assist our understanding of probability and betting.
In statistics, the odds in favour, sometimes known as just the odds, of an event is the ratio of the probability of the event occurring to the probability of the event not occuring. If p is the probability of an event occurring, then the odds for that event are given by:
For example, if the probability of event A occurring is 0.4, then the odds of event A are 2/3. Similarly, the odds against an event is the ratio of the probability of the event not occurring to the probability if the event occurring. If the odds of event A are odds(A) and the odds of event B are odds(B), then we define the odds-ratio of A to B as
The odds-ratio measures the relative probability of two events. If the odds ratio of A to B is 2, then we will say that event A is twice as likely as event B. To illustrate, consider the difference between 50% and 51%, and 98% and 99%. In absolute terms, the difference between the two numbers in each pair is 1%, but it’s clear that intuitively the difference between 98% and 99% is much greater than the difference between 51% and 50%. The odds-ratio of 51% to 50% is 1.04, but the odds-ratio of 99% to 98% is 2.02, thus showing that the difference is indeed much greater. Also, while we might instinctively want to say that 60% is twice as likely as 30% (because 60/30 = 2), there is no answer to the question of what is twice as likely as 60% using this definition. But using the odds-ratio, we can say that 75% is twice as likely as 60%, because OR(75%, 60%) = 2.
One application of the odds and odds-ratio is to the bookmaker’s distribution of the overround, a concept that represents the bookmaker’s profit margin. Consider an event in a betting market that can only have one winner from n selections with bookmaker prices o1, o2, …, on. The overround v is defined as the sum of the inverse of the odds:
The overround represents the amount the bookmaker would need to lay in order to make a payout of exactly 1 unit of currency, assuming the stakes are distributed in the correct proportions across the selections. To illustrate, for v = 1.081, if the bookmaker laid £10.81 in the correct proportions, then they would pay out £10.00 to the punters. Another important concept, related to the overround, is the margin m of a betting market, defined as the bookmaker’s profit as a percentage of the turnover, assuming the stakes are distributed in the correct proportions. The margin is related to the overround as follows:
How any bookmaker sets the price (relative to the true price) to make a profit obviously varies, but with the advent of automated models in betting, having an algorithmic method of distributing the overround is desirable.
Consider for simplicity a general two-way market, consisting of selections having true probabilities p and q = 1 − p, so that p + q = 1. When distributing the overround algorithmically, ideally we require functions f and g that act on p and q, respectively, such that f(p) +g(q) = v, where v is the overround. One such choice is f(p) = vp and g(q) = vq (then f(p) + g(q) = vp + vq = v, so the condition is satisfied). This method is in fact called proportional distribution, and represents simply dividing the true odds by the required overround. The method is well-known because of its simplicity, but produces final probabilities greater than one if the true probabilities are high enough. Another method is to add the overround equally between both probabilities, so that f(p) = p + 0.5(v − 1) and g(q) = q+0.5(v−1). Again the overround condition is satisfied. This method seems to be better than proportional distribution but again suffers from the problem of probabilities exceeding 1. Another method, which ensures the final probabilities are always between 0 and 1, involves the use of the odds and the odds-ratio.
Suppose that the overround functions f and g takes the true probabilities p and q to the new probabilities x and y, respectively. A sensible method of distributing the overround might require that the difference between p and x, and q and y, is in a sense ‘equal’. The method we introduce now will ensure this by requiring equal odds-ratio between each pair of old and new probabilities, in the sense that
Suppose the odds-ratios are equal to c. Then
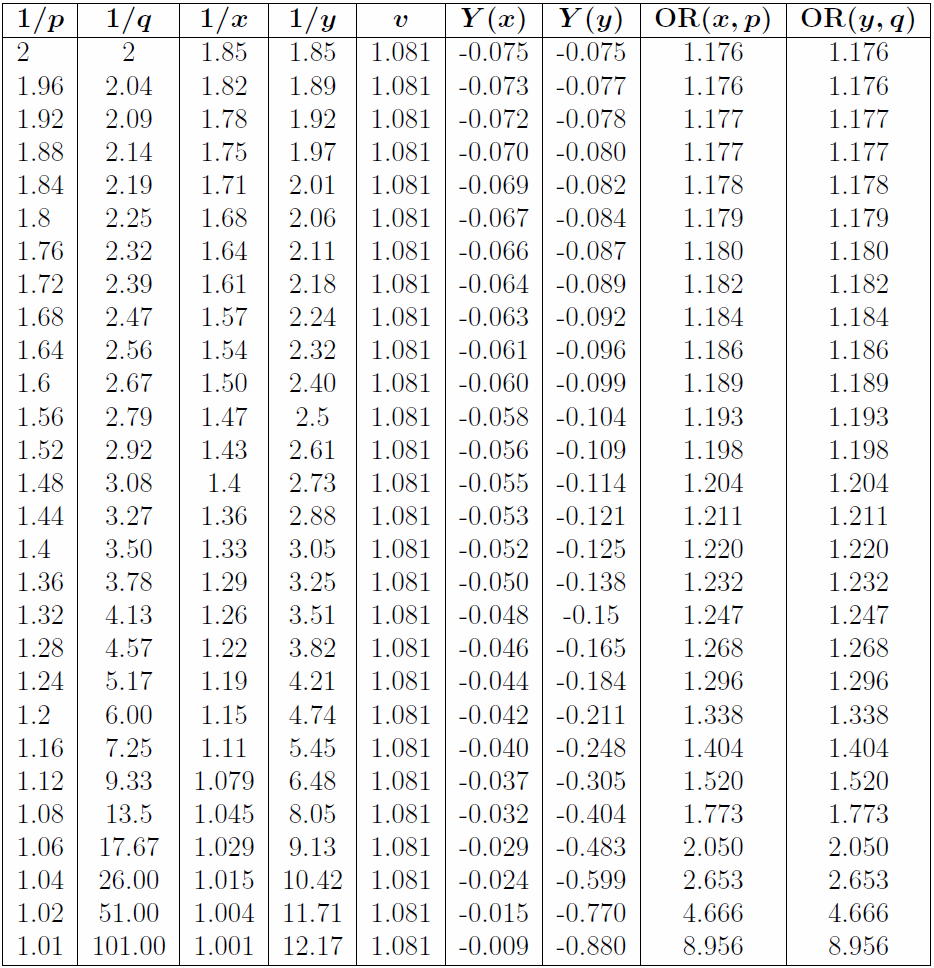
If we set x + y = v, then we can solve for c, and hence get final expressions for x and y. The following table gives the true odds and the new odds using the above distribution method for a two-way market with margin 0.075.
Note that, of course, the overround is the same for every pair of odds. Y is the (punter’s) yield, or rate of return, which is the expected profit or loss on a punter’s bet as a proportion of the stake. If o are the bookmaker odds and ot are the true odds, then the yield is given by
So if a punter bets £1 at the price of 1.5 on something with true odds of 1.6, the yield is −0.06 or −6% and he will on average get back £0.94. Notably, using this method of distributing the overround, bets on shorter odds will generate a higher rate of return in comparison to bets on longer odds. Also, the odds-ratios of x to p and of y to q are equal, as is required, and they increase as the probabilities deviate from evens. This means that, for example, the difference between (1.08, 13.5) and (1.045, 8.05) is ‘bigger’
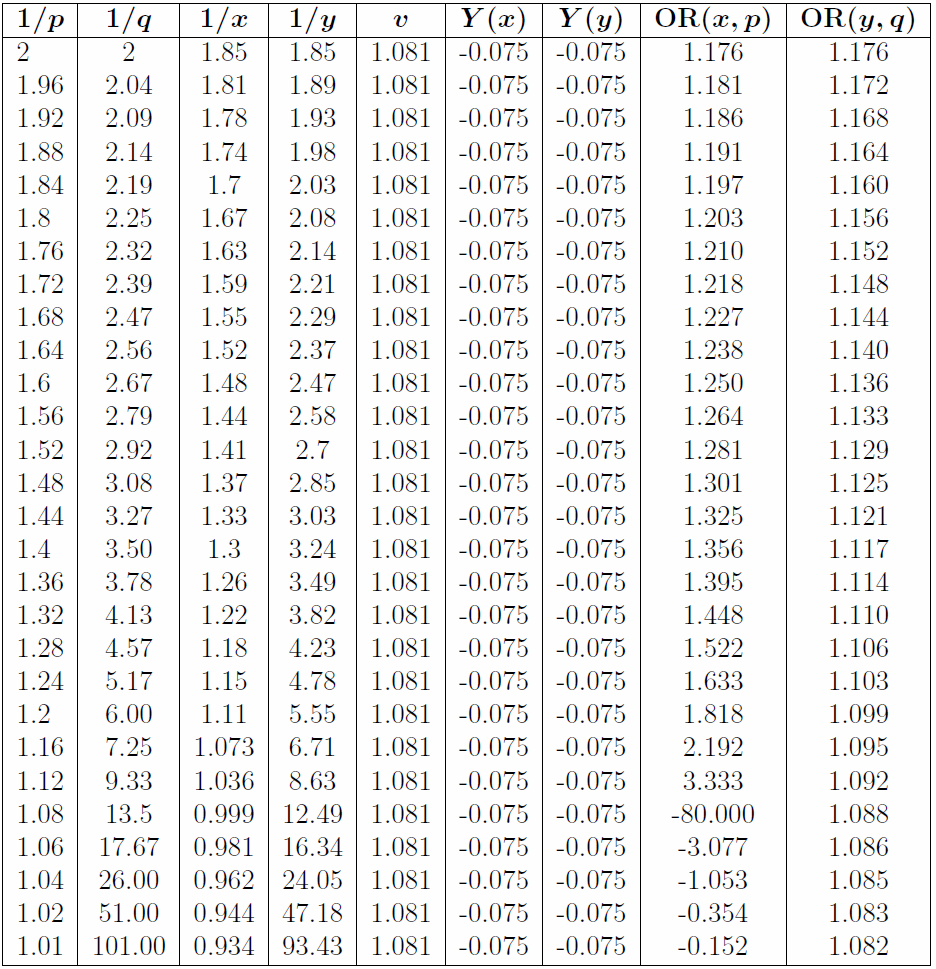
than the difference between (1.8, 2.25) and (1.68, 2.06) – even though the overrounds are equal – so that markets with shorter odds have poorer ‘value’ in comparison to markets with more balanced odds, if they have the same overround. To compensate for this, some bookmakers lower the overround progressively as probabilities reach the tails. In addition to distributing the overround, we can also use this method to remove the overround. Now let’s compile the same table for proportional distribution, again with margin 0.075.
Again, the overround for every pair of odds is the same. The bookmaker’s yield for every selection is precisely the margin; this is the key feature of proportional distribution. With proportional distribution, it’s clear that too much of the overround is being put on the favourite and not enough on the underdog, eventually giving rise to probabilities greater than 1. Looking at the odds-ratios can help us understand what is going on: we see that they increase as the odds shorten, turning negative as the odds become less than one; and decrease as the odds get longer, meaning the new odds become very close to the true odds.
If a bookmaker wants the odds to be such that any unit stake has the same rate of return no matter the odds, the only way to achieve this is by proportional distribution, but this is clearly a poor way to set the odds. As we have seen, equal odds-ratios is a better way to set the final odds, but (at least in the two-way case) necessarily has the feature that punters’ bets on shorter odds generate a higher rate of return than bets on larger odds; also, the yield strictly increases as the odds shorten. It appears likely that equal odds-ratio will give rise to this phenomenon regardless of the number of selections in the event. The feature that bets on shorter odds generate a higher rate of return than bets on longer odds is sometimes known as the favourite–longshot bias. It seems reasonable that the primary reason the favourite–longshot bias exists in fixed-odds betting markets is because of the way bookmakers set their odds: setting the odds in what a bookmaker might consider a sensible manner (and taking into account any factors that might influence the odds) will likely produce final odds that feature the longshot bias.