Related Articles
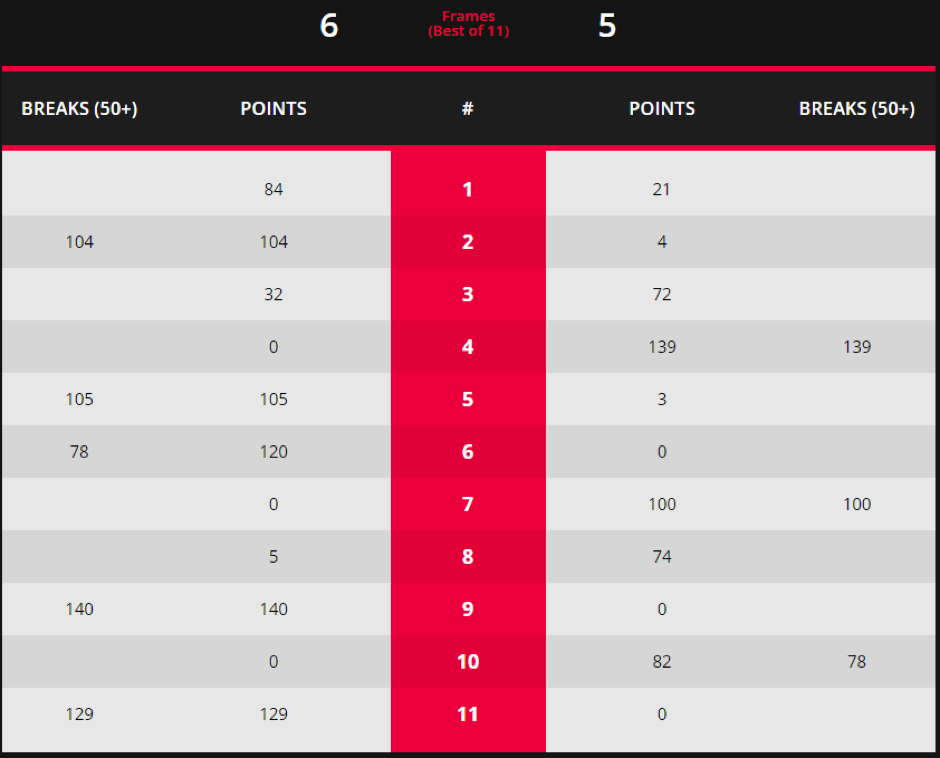
The recent Masters quarter final between Judd Trump and Neil Robertson was a match of exceptional quality. Spectators knew that they were witnessing something special as each player fired in a string of high breaks, among them a total of 6 centuries from the 11 completed frames. I was among those spectators, thanks to the generosity of the good people of Sports Trading Network. As I watched the drama unfold, I mused upon the likely outcome for both fixed odds firms and spread betting ones alike. Extreme outcomes can often be calamitous for the latter in particular. But how rare are these examples of high scoring and how might we calculate their likelihood?
Fortunately, we are blessed in the modern age with plenty of data from which we can make reasonable assumptions. One such source, the excellent www.cuetracker.net reveals that Trump makes a century in about 17% of the frames that he wins, while Robertson has a slightly better strike rate of about 18%.
Armed with this knowledge, and the fairly safe assumptions that you can only make one century per frame, and that the frame will always be won by the person making the century, we can apply the binomial probability function to the variables surrounding the match.
This function enables us to establish the distribution of the number of successes in a sequence of independent trials, each of which yields success with a constant probability – or in plain English, it helps us find the chances of a given number of centuries in the match.
Robertson was deemed to be a small favourite for the match among the betting fraternity at about 1.72 (58%), with an implied chance of 53% of winning each frame. The 53% frame variable is the last piece of information that we need, as we can now construct probabilities for each scoreline, and from that, the likelihood that a certain amount of centuries might be scored given each possible scoreline.
The problem then becomes one of combining all the different possible outcomes and adding them together. This is shown in the chart below:
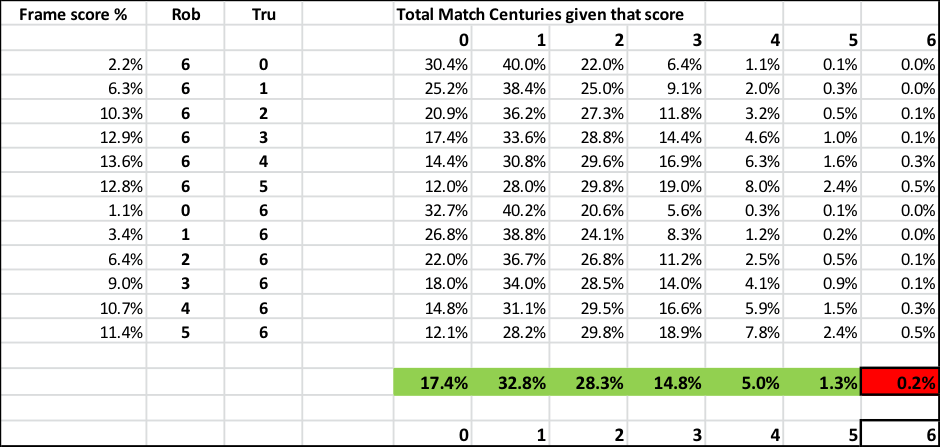
Using this method of calculation, it is suggested that the chance of Trump and Robertson sharing 6 centuries in their match given their respective abilities and scoring rates, was approximately 0.2%, or about a 500/1 chance.
As readers will know, the binomial distribution is not a perfect way to calculate probabilities, but it is a reasonably good fit as you can see from the following graph, which displays the outcomes of all the best of 11 Masters snooker matches up to 2015, and the expected probabilities using the binomial probability function:
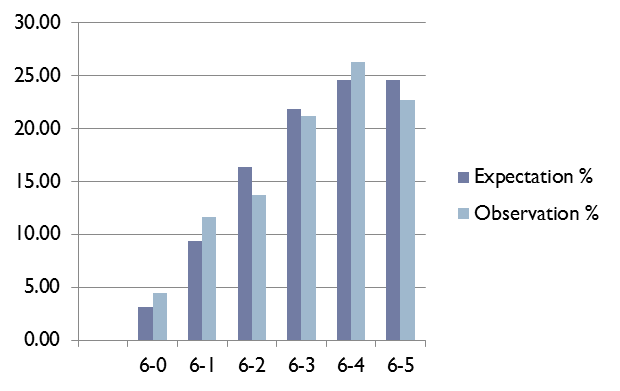
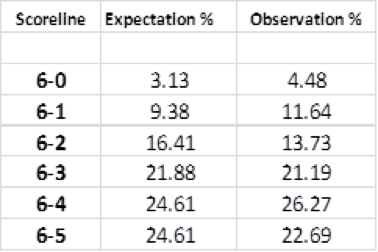
For the record, I must state that I made an assumption that in all frames each player had the same 0.5 probability of winning (which of course isn’t true in the real world), but given that the Masters is a tournament of the highest quality, it’s not the worst piece of statistical skulduggery ever proposed in order to illustrate a point. In any event, assuming this constant probability demonstrates that, from an odds-compiler’s perspective, the function is a handy tool to lead us to reasonable estimates. More sophisticated models used by bookmakers and B2B suppliers would doubtless include variables to account for momentum and the like. An obvious drawback of the binomial distribution is that the probability of success/failure is assumed to be constant in each frame (trial), when in fact we know the form of players does in fact fluctuate and is often subject to sharp swings in momentum.
By way of some proof, these unlikely events do seem to happen more often than the maths suggests. This is probably down to the fact that we might calculate a player’s chances by his historical constant average, when in fact from time to time he will significantly over-perform or under-perform on the way to that average. This is likely to skew the probability distribution at both ends and make extremely good (and extremely bad) performances slightly more likely than we might expect. As if to bolster this suggestion, Kyren Wilson and Anthony Hamilton shared a record-breaking six centuries in consecutive frames in their recent China Open qualifying match.
Of course, regardless of the exact probability, those who were lucky enough to watch either of those matches will remember them for many years to come precisely because such extraordinary quality is a rarity that will not go unforgotten. So I salute Alun, Brooke and their colleagues for selecting such an excellent prize for the runners-up at the MathSport International Quiz held at Loughborough University in 2015 http://www.mathsportinternational.com/previous.html) – it was a match to remember.